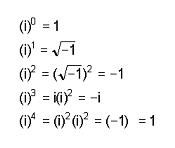C no puede ser convertido de ninguna manera en un cuerpo ordenado.

Aplicaciones de los numeros complejos ejemplos.
Aplicaciones de los numeros complejos en la ingenieria civil materia.
En su versión original se los define a través de cálculos con números complejos en el plano.
5 3 i.
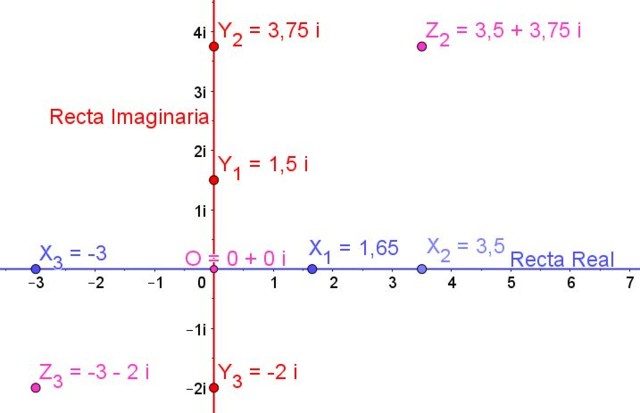
En dicho plano complejo los valores reales están represen tad os en el eje horiz ontal y los valores imaginarios en el eje vertical.
Los complejos no pueden ser ordenados como por ejemplo los números reales.
2 7 i 3 4 i 2 3 7 4 i.
Una aplicación sencilla de los números complejos es hallar todas las raíces de una ecuación polinómica como la que se muestra al principio del artículo.
Conjugado de un número complejo dos binomios se llaman conjugados si solo difieren en su signo central por ejemplo los dos binomios.
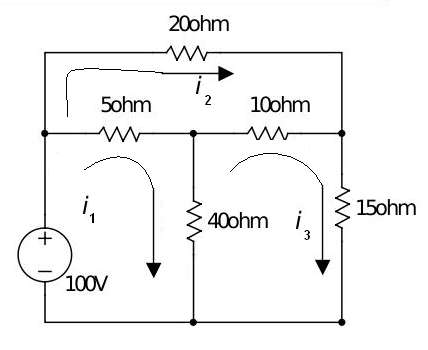
Aplicación de los números complejos en la ingeniería por saul rivero 1.
Para sumar dos números complejos sume la parte real a la parte real y la parte imaginaria a la parte imaginaria.

En una expresión del tipo zr ei phi podemos pensar en r como la amplitud y en phi como la fase de una onda sinusoidal de una frecuencia dada.
4 3i 6 5i 1 i 2 4i.
Operaciones con números complejos.
Aplicaciones de los números complejos los números complejos se usan en ingeniería electrónica y en otros campos para una descripción adecuada de las señales periódicas variables.
El término número complejo describe la suma de un número real y un número imaginario que es un múltiplo real de la unidad.
3m 1 y.
Donde atan2yx es la función arcotangente definida para los cuatro cuadrantes.
Algebra resumen un complejo es una entidad que viene dada por un par de iniciar sesión regístrate ocultar.
En el caso de la ecuación x 2 10x 34 0 al aplicar la fórmula resolvente se obtiene.
Un número complejo es una entidad matemática que viene dada por un par de números reales el primero x se denomina la parte real y al segundo y la parte imaginarialos números complejos se representa por un par de números entre paréntesis x y como los puntos del plano o bien en la forma usual de xyi i se denomina la unidad imaginaria la raíz cuadrada de menos uno.

El argumento principal o fase de un número complejo genérico siendo xrez e yimz viene dado por la siguiente expresión.
E n la imagen de la izquierda tenemos algunos ejemplos de números complejos.
Para restar dos números complejos reste la parte real de la parte real y la parte imaginaria de la parte imaginaria.
Ya que pueden calcular integrales reales que métodos normales no pueden bibliografía.
Los números complejos se usan en ingeniería electrónica y en otros campos para una descripción adecuada de las señales periódicas variables ver análisis de fourier.

Aquí está la información completa sobre aplicaciones de los numeros complejos ejemplos. El administrador del blog Nuevo Ejemplo 10 January 2019 también recopila otras imágenes relacionadas con los aplicaciones de los numeros complejos ejemplos a continuación.